因子分解机 Factorization Machine
因子分解机主要是考虑了特征之间的关联。
FM主要是为了解决数据稀疏的情况下,(而SVM无法解决稀疏问题),特征怎样组合的问题。
数据稀疏是指数据的维度很大,但是其中为0的维度很多。推荐系统是常见应用场景,原因是推荐系统中类别属性(如商品id)比较多,每一种类别属性经过onehot处理后会产生大量值为0的特征,导致样本变得稀疏,而FM就可以解决这种样本稀疏的问题。
因子分解机FM算法可以处理如下三类问题:

普通线性模型
我们将各个特征独立考虑,并没有考虑特征之间的相互关系。
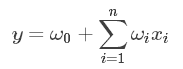
FM模型
为了表述特征间的相关性,我们采用多项式模型,将特征$x_i$和$x_j$的组合用$x_ix_j$表示,只讨论二阶多项式模型:
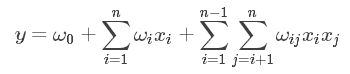
其中,n表示样本的维度(是已经进行onehot以后的特征数量),$x_i$表示第i个特征,(如果是类别变量,那么onehot后只有一个维度值为1,其余维度值为0,因此在这种情况下$x_i$的值通常是取0和1,而对于一般的数值维度,$x_i$的值对应原来的数值), $w_{ij}$是组合参数,代表组合特征的重要性,注意:$w_{ij}$和$w_{ji}$是相等的,因此组合特征部分相关参数共有$(n-1)+(n-2)+…+1=n(n-1)/2$
注意到,在数据稀疏的情况下,满足特征$x_i$和$x_j$都不为0的情况很少,因此$w_{ij}$很难训练。
为了求解组合参数$w_{ij}$, 对每个特征分量$x_i$引入k维(k远小于n) 的辅助向量$v_i=(v_{i1}, v_{i2},…,v_{ik})$, 然后利用向量内积的结果$v_iv_j^T$来表示原来的组合参数$w_{ij}$
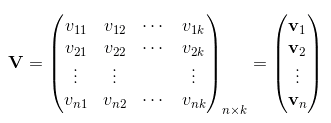
实际上,辅助向量可以理解为是特征分量的另一种表示形式,类似于词向量的表示形式,但是和词向量存在区别。词向量中是将一个单词转换为向量表示形式,而单词是固定的,因此一个单词对应一个词向量;而在FM中,我们是将一个类别特征(注意,这是onehot前的特征)转换为一个向量,但由于该类别特征可以有多种取值,并且每种取值对应一个向量(也就是上面将类别特征onehot以后,每个特征分量对应一个辅助向量),因此,FM中确实是将一个类别特征转换为了向量形式,只不过向量会根据特征的取值发生变化。
此时,组合参数$w_{ij}$组成的矩阵可以表示为:
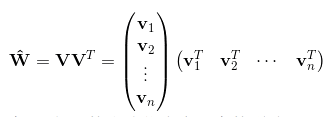
将组合参数进行分解的好处:
- 从原来要求n(n-1)/2个组合参数变成了求矩阵V,参数数量变为n*k.
- 削弱了高阶参数间的独立性:k越大(即对特征分量的表征能力越强),高阶参数间独立性越强,模型越精细;k越小,泛化能力越强,
因此实际问题选择较小的k可以克服稀疏数据的问题,并获得较好的预测效果。
因此时间复杂度从O(n^2)变成了O(kn)
此时,分解机的表示形式变为:
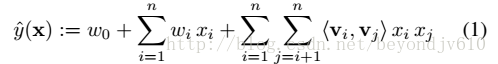
注意第二项,下标j的循环从i+1开始。
使用辅助向量乘积表示组合参数的原理:
通常,由于数据稀疏,本来组合参数是学习不到的,但是我们可以通过特征i与其他特征的数据的关系,特征j和其他特征的关系,分别学习到特征i和特征j的对应的辅助向量$v_i$和$v_j$,这样利用$v_iv_j^T$来表示$w_{ij}$,便可以解决数据稀疏带来的问题。
计算模型的预测值:
在计算模型时,只需要考虑计算量最大的二次项:
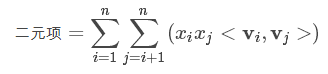
可以先把标量$x_i$和对应的辅助向量$v_i$相乘,并记录下来,得到$u_i=x_iv_i$, 注意$x_i$只是标量。
对于n个元素,共需要nk次乘法,于是二元项变为:注意:*公式中的r即为k,即辅助向量的维度
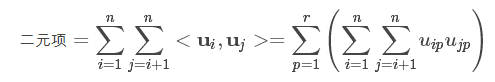

把上式凑成和的平方:
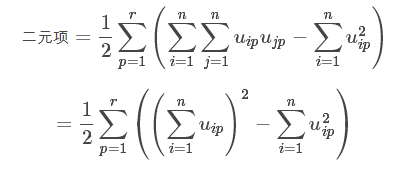
化简的原理是将整个对称矩阵W除去对角线上的数值,由于对称,再除以2得到原来的上三角矩阵。
括号内,两部分计算量均为O(n),因此整体计算量为O(kn)。
梯度下降求解模型参数:
SGD中,需要计算两种导数:
- 预测值对一元参数的导数:
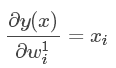
- 预测值对二元参数的导数:
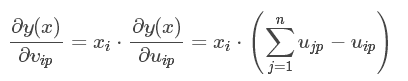
实际处理问题:
回归问题:
在回归问题中,直接使用模型预测值作为预测结果,并使用最小均方误差作为损失函数,其中m为样本个数:
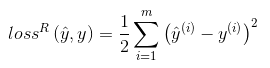
二分类问题:
将输出结果通过激活函数,如sigmoid函数得到预测类别的概率,使用对数似然作为损失函数:
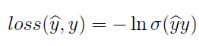
场感知分解机 FFM
FM的应用场景:给定一组数据,判定用户是否会进行点击。
采用onehot对categorical类型的数据进行编码后,数据会十分稀疏,并且数据维度增大。
以广告分类为例,“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征都是代表日期的,可以放到同一个field中。同理,商品的末级品类编码生成了550个特征,这550个特征都是说明商品所属的品类,因此它们也可以放到同一个field中。简单来说,同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field,包括用户性别、职业、品类偏好等。
Field-aware Factorization Machine(FFM) 模型
场感知说白了可以理解引入了field的概念,FFM把相同性质的特征归于同一个field。
因此,隐向量不仅与特征相关,也与filed相关,
即:对每一维特征分量$x_i$, 针对每一种field $f_j$ , 都会学习一个隐向量$v_{i, f_j}$,与不同的特征关联需要使用不同的隐向量 (而FM每种特征只有一个隐向量)
例如,当考虑“Day=26/11/15”这个特征,与“Country”特征和“Ad_type”特征进行关联的时候,需要使用不同的隐向量,而在FM中则使用相同的隐向量。
假设样本的n个特征(已经onehot)属于f个field, 那么FFM二次项有nf个隐向量。
因此,得到:
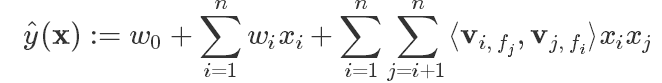
其中,$f_j$是第j个特征所属的field. 如果隐向量的长度为k, 那么FFM的交叉项参数就有nfk个,远多于FM模型的nk个。此外,由于隐向量于filed有关,FFM的交叉项并不能够像FM那样进行化简,预测复杂度为$O(kn^2)$.
FFM的使用:所有的特征必须转换成“field_id:feat_id:value”格式,field_id代表特征所属field的编号,feat_id是特征编号,value是特征的值.
在FFM论文版本里的梯度更新,学习率是通过类似于adagrad自适应的学习率计算的。根据AdaGrad的特点,对于样本比较稀疏的特征,学习率高于样本比较密集的特征,因此每个参数既可以比较快速达到最优,也不会导致验证误差出现很大的震荡。
参考:
FM算法详解:https://blog.csdn.net/bitcarmanlee/article/details/52143909
FM计算:https://blog.csdn.net/shenxiaolu1984/article/details/78740481
fm美团:https://tech.meituan.com/deep_understanding_of_ffm_principles_and_practices.html
csdn, 推荐算法:https://blog.csdn.net/asd136912/article/details/78318563
美团,FFM: https://tech.meituan.com/deep_understanding_of_ffm_principles_and_practices.html