BPR 贝叶斯个性化排序

显式反馈：用户对物品的评分，如电影评分
隐式反馈：用户对物品的交互行为，如浏览，购买等，现实中绝大部分数据属于隐式反馈，可以从日志中获取。
BPR是基于用户的隐式反馈，为用户提供物品的推荐，并且是直接对排序进行优化。

定义

$U$代表所有的用户user集合；

$I$代表所有的物品item集合；

$S$代表所有用户的隐式反馈，$S \subseteq U \times I$. 如下图所示，只要用户对某个物品产生过行为，就标记为$+$, 所有$+$样本构成了$S$。那些未观察到的数据（即用户没有产生行为的数据）标记为$?$.

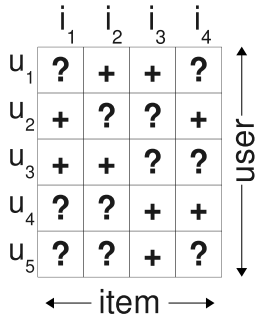
$i>_uj$表示用户u在物品i和物品j之间更偏向于物品i

$I_u^+=\{i \in I: (u,i) \in S\}$ 代表了用户u产生过行为的物品集合

$U_i^+=\{u \in U: (u,i) \in S\}$ 代表了对物品i产生过行为的用户集合

传统解决方式

在使用隐式反馈的情况下，我们会发现观察到的数据均为正例（因为用户对物品交互过才会被观察到），而那些没有被观察到的数据（即用户还没有产生行为的物品），分为两种情况，一种是用户确实对该物品没有兴趣（负类），另一种则是缺失值（即用户以后可能会产生行为的物品）。

传统的个性化推荐通常是计算出用户u对物品i的个性化分数$\hat{x}_{ui}$,然后根据个性化分数进行排序。为了得到训练数据，通常是将所有观察到的隐式反馈$(u,i) \in S$作为正类，其余所有数据作为负类，如下图所示，左图为观察到的数据，右图为填充后的训练数据：

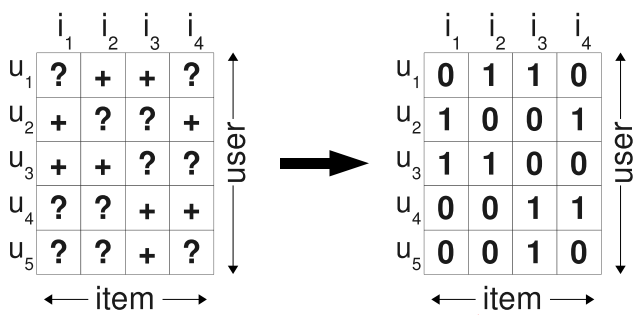
在填零的情况下，我们的优化目标变成了希望在预测时观测到的数据预测为1，其余的均为0. 于是产生的问题是，我们希望模型在以后预测的缺失值，在训练时却都被认为是负类数据。因此，如果这个模型训练的足够好，那么最终得到的结果就是这些未观察的样本最后的预测值都是0。

BPR的解决方式

BPR采用了pairwise的方式。

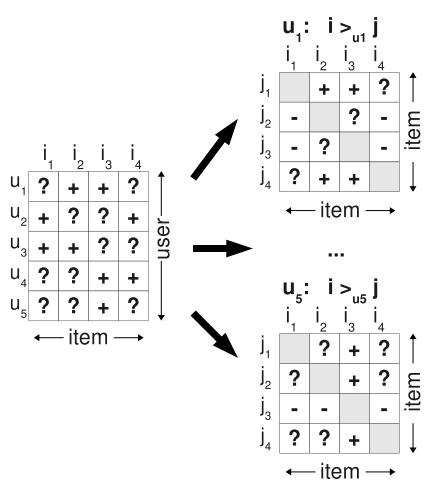
如 下图，基于观察到的数据S构建数据集$D_S$: 对用户u来说，如果对物品i产生过行为（即$(u,i) \in S$), 而没有对物品j产生过行为，则得到了一个偏好对$(u,i,j)$。如对用户$u_1$来说，对物品$i_2$产生过行为，而没有对物品$i_1$产生过行为，则得到了用户$u_1$的一个偏好对$(u_1, i_2, i_1)$, 或者表示为$i_2>_{u1}i_1$. 如果一个用户对两个物品同时产生过行为，或者同时没有产生过行为，则无法构建偏好对。接着，对每个用户，就可以构建$I \times I$的偏好矩阵。所有用户的偏好对构成了训练集$D_S: U \times I \times I$

$$D_S=\{(u,i,j)|i \in I_u^+ \land j \in I \backslash I_u^+\}$$

注意，对每个三元组样本$(u,i,j)​$, i必然是产生过行为的物品，j必然是未被产生过行为的物品，因此$D_S​$只包括下图右边分解后为$+​$的数据，不包含$-​$的数据。

BPR-OPT

BPR基于最大后验概率, 对每一个用户u而言，后验概率正比于似然概率乘上先验概率：

$$p(\theta|>_u) \propto p(>_u|\theta)p(\theta)$$

其中，$>_u$表示了用户u对所有物品的偏好关系。下面从分解后的似然概率和先验概率做出解释。

似然概率

独立性假设：

1. 所有用户之间的行为相互独立
2. 同一用户任意一对物品的偏序关系相互独立

于是可以将似然概率表示为（这里跳过了包含负例部分的分解，原论文这部分关于负例的表示让我有些疑惑，有兴趣的可以参见下这篇博客的讨论部分）：

$$\Pi_{u\in U}p(>_u|\theta)=\Pi_{(u,i,j) \in D_S}p(i>_uj|\theta)$$

即分解为每一个正样本的概率之积，即我们希望对每一个正样本$(u,i,j) \in D_S$, $p(i>_uj|\theta)$最大。这里不考虑负样本。

这里定义：

$$p(i>_uj|\theta):=\sigma(\hat{x}_{uij}(\theta))$$

其中$\sigma$是sigmoid函数，$\sigma(x)=\frac{1}{1+e^{-x}}$

$\hat{x}_{uij}(\theta)$是个实值函数，返回的是用户u, 物品i, 物品j之间的关系。这个函数可以通过矩阵分解或者KNN等方法实现。

先验概率

这里假设了参数的先验概率服从正态分布

$$p(\theta) \sim N(0, \lambda_\theta I)$$

对于正态分布，其对数和$||\theta||^2$成正比。因此计算$lnp(\theta)$时，得到：

$$lnp(\theta)=\lambda||\theta||^2$$

后验概率

得到似然概率和先验概率后，最终得到后验概率。取对数得到优化目标。

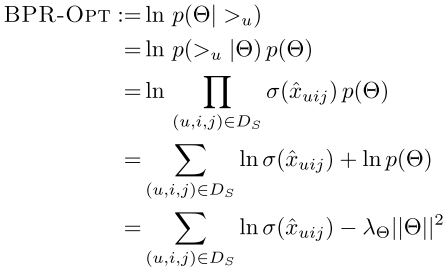
先验概率相当于正则项，由于假设了高斯分布，因此变为L2正则。

梯度下降

由于优化函数可微，因此采用梯度下降法。

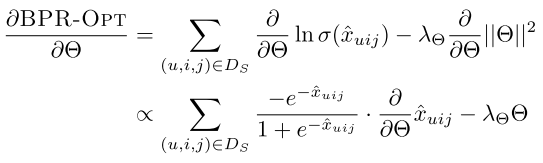
采用随机梯度下降：

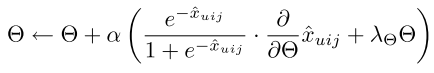
基于矩阵分解的BPR

矩阵分解的作用主要就是为了得到上述的实值函数$\hat{x}_{uij}(\theta)$.

对于用户集$U$和物品集$I$对应的$U \times I$的预测的排序矩阵$\hat{X}$, 我们期望分解得到用户矩阵$W (|U|\times k)$和物品矩阵$H (|I| \times k)$, 满足：

$$\hat{X}=WH^T$$

这里的k是自己定义的，对于用户矩阵W, 我们实际上就是为每一个用户u学出一个k维向量$w_u$作为该用户的隐向量，同理，对于物品矩阵H, 我们实际上就是为每一个物品i学出一个k维向量$h_i$作为该物品的隐向量。

因此，这里的$(W, H)$实际上就是我们需要求出的参数$\theta$. 为方便，下面式子不再写$\theta$

当得到W和H矩阵后，对于任意一个用户u，对应的任意一个物品i, 得到的实值向量即为两个隐向量之积：

$$\hat{x}_{ui}=w_u \cdot h_i=\sum_{f=1}^kw_{uf}h_{if}$$

$\hat{x}_{ui}$的物理意义可以理解为是预测出的用户u对物品i的评分。

但是BPR中是三元组形式的$\hat{x}_{uij}$,因此BPR将三元组形式分解为二元组的形式，定义为：

$$\hat{x}_{uij}=\hat{x}_{ui}-\hat{x}_{uj}$$

同时，上面这个式子满足了：当$i>_uj$时，$\hat{x}_{uij}>0$;当$j>_ui$时，$\hat{x}_{uij}<0$.

代入后验概率模型，得到：

$$lnp(\theta|>_u)=\sum_{(u,i,j)\in D_S}ln\sigma(\hat{x}_{ui}-\hat{x}_{uj})+\lambda||\theta||^2$$

根据上节梯度下降更新梯度，得到：

$$\theta \leftarrow \theta + \alpha(\frac{1}{1+e^{\hat{x}_{ui}-\hat{x}_{uj}}} \cdot \frac{\partial}{\partial \theta}(\hat{x}_{ui}-\hat{x}_{uj})+\lambda\theta)$$

其中：

$\hat{x}_{ui}-\hat{x}_{uj}=\sum_{f=1}^kw_{uf}h_{if}-\sum_{f=1}^kw_{uf}h_{jf}$

于是，可以得到：

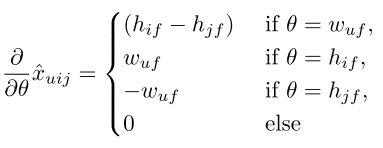
接下来就可以更新参数了。

当然，除了采用矩阵分解的方式实现，也可以使用KNN的方式去实现$\hat{x}_{uij}$, 具体可参见论文。

尽管BPR采用的仍然是矩阵分解的方式，但传统的矩阵分解主要是去尝试拟合$\hat{x}_{ui}$, BPR的优化角度是直接对排序进行优化，相当于对差值$\hat{x}_{ui}-\hat{x}_{uj}$进行分类，因此更加有效。

参考：

Rendle, et.al., BPR: Bayesian Personalized Ranking from Implicit Feedback

刘建平博客：https://www.cnblogs.com/pinard/p/9128682.html#commentform

其他:

在上传这篇博客到hexo时,由于公式太多,导致了网上公式渲染出现问题,非常感谢在Hexo中渲染MathJax数学公式提出的方法.