ALS 交替最小二乘

发表于 | 分类于 |

ALS算法是矩阵分解的一种，用于评分预测。

矩阵分解

假设我们有一批用户数据，其中包含m个User和n个Item, 用户和物品的关系是一个三元组，, 即用户对物品的评分，因此我们得到矩阵$R_{m\times n}$, 其中的元素$r_{ui}$表示第u个用户对第i个item的评分。

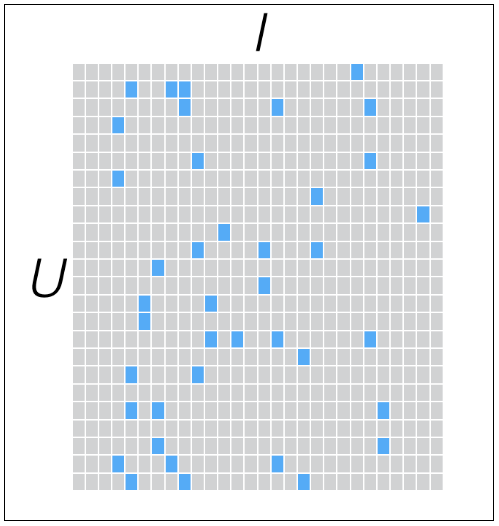
1538020000484

评分矩阵通常规模很大，并且通常是稀疏矩阵，因为一个用户不可能给所有商品评分。矩阵中缺失的评分，称为missing item.

接下来将这个矩阵分解为两个子矩阵，使得两个子矩阵能近似得到原矩阵：

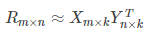
1538020213031

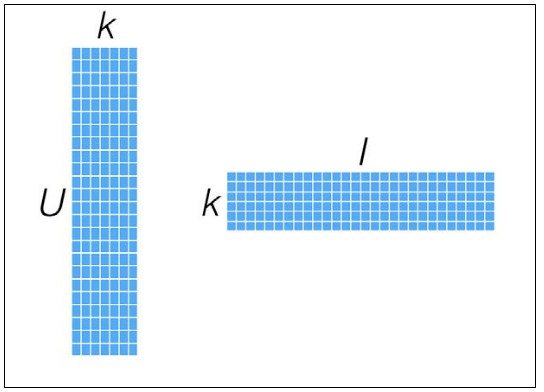
如下图所示，左边X矩阵实际代表用户的隐矩阵，即每个用户用一个k维向量表示，而右边的矩阵代表物品的隐矩阵，即每个物品用一个k维向量表示。k的值通常远小于n和m.

1538020466589

为了使低秩矩阵XY的乘积接近于R, 得到了我们的目标函数：

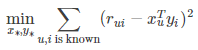
1538020553627

通常加入正则项，得到：

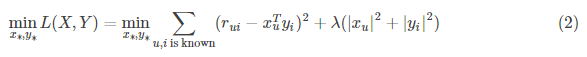
1538020590139

我们的目标就是优化上式，得到训练结果X, Y。预测时，我们只要将User和Item代入$r_{ui}=x_u^Ty_i$就能得到相应的评分预测值。

此外，由于训练出了每个用户和物品的隐向量，因此根据向量比较User和Item之间的相似度。

ALS优化

直接优化公式2比较困难，因此需要用ALS中的核心概念：交替。先固定其他维度，只优化其中一个维度。

对$x_u$求导，将$y_i$当作常量，可得：

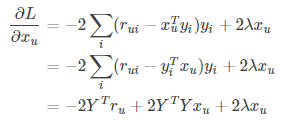
1538020965623

令导数为0，可得：

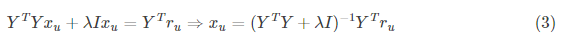
1538021322942

同理，对$y_i$求导，由于X和Y是对称的，得到：

1538021355541

因此，整个迭代优化过程为：

  1. 随机生成X, Y

    repeat until convergence {

  2. 固定Y, 使用公式3更新$x_u$

  3. 固定X, 使用公式4更新$y_i$

    }

一般使用RMSE评估误差是否收敛：

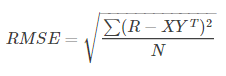
1538021531707

算法复杂度：

  1. 求$x_u$:$O(k^2N+k^3m)$

  2. 求$y_i$:$O(k^2N+k^3n)$

可以看出来当k一定的时候，这个算法的复杂度是线性的。

因为这个迭代过程，交替优化X和Y，因此又被称作交替最小二乘算法（Alternating Least Squares，ALS）。

ALS与隐式反馈

隐式反馈与ALS的结合，有ALS-WR算法，即加权的ALS算法。

显示反馈：用户对商品的评分。

隐式反馈：用户对商品的行为，如点击，收藏，搜索，购买记录等。

隐式反馈的特点：

  1. 没有负面反馈，用户一般会直接忽略不喜欢的商品，而不是给予负面评价

  2. 隐式反馈包含大量噪声

  3. 隐式反馈难以量化

  4. 显式反馈表现的是用户的喜好（preference），而隐式反馈表现的是用户的信任（confidence）。比如用户最喜欢的一般是电影，但观看时间最长的却是连续剧。大米购买的比较频繁，量也大，但未必是用户最想吃的食物。

参考：

csdn: https://blog.csdn.net/antkillerfarm/article/details/53734658